Check if a Collection has Changed

Assume two hash-indexed collections $A$ and $A'$ exist and that collection $A$ from a previous state must be compared to collection $A'$ from the current state. The task is to find an efficient method to:

  1. check if the new collection $A'$ contains exactly the same elements from the previous state $A$,
  2. update collection $A$ to contain the elements from the new collection $A'$ without disposing of the contents of collection $A$

For the exercise you are allowed to use only comparisons, set operations and not allowed to introduce intermediary variables.

Solution

(1) Given the two sets, initial set $A$ and new set $A'$, the intersect can obtained via $A \cap A'$ and the result assigned to $A$ such that $A$ will contain only the elements common to both $A$ and $A'$. Since the exercise mentions hash-indexed collections, one can assume that $A$ and $A'$ are proper mathematical sets with no duplicate elements, such that using a simple length comparison between $A$ and $A'$ will reveal whether the sets are equal. (2) Finally, since $A$ now contains elements in both $A$ and $A'$, an union can be performed between $A$ and $A'$ and assigned to $A$ which will yield a set that contains the elements of $A$ and any new elements in $A'$.

Summarized:

\begin{eqnarray*} A &=& A \cap A' \\ A_{len} &\mathtt{compare}& A_{len} \\ A &=& A \cup A' \\ \end{eqnarray*}

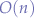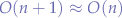For the first point (1), the time complexity would be $O(n)$, the comparison is an $O(1)$ operation such that the first point carries an overall complexity of $O(n + 1) \approx O(n)$. The second point (2) also requires 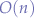$O(n)$ time complexity.